C++11 / Boost: Multi-threading – The Parallel Aggregation Pattern

In the first part of this series we looked at general multi-threading and multi-core programming concepts without getting into the meat of any real problems. Tutorials on how to spin up worker threads in C(++) using POSIX/Pthreads, Windows or Boost.Thread are a dime a dozen so I won’t spend too much time on that here; instead I’ll look at a much less-documented and more complicated real-world multi-threading problem, namely that of parallel aggregation, and how to implement it both using new C++11 standard library functions, and with Boost.Thread for those who don’t have access to C++11 at present.

In the example developed in this article, we shall learn how to add all of the numbers from 0 to 1,000,000,000 (1 US billion) exclusive, using multi-threading on a multi-core system to speed up execution and make all the available cores work for us, rather than just one.

(do note that this particular problem can be solved very simply with the sum of a series formula: S = n(a₁ + a_n) / 2 where S is the sum of the series, a_x is the x‘th term in the series and n is the number of terms in the series; we are using the brute-force approach here purely for illustration)

What is Parallel Aggregation?

Figure 1. Adding all the numbers in a contiguous sequence in a single-threaded application

You have a long-running, time-consuming calculation or process you wish to execute, but you want to split the execution across multiple threads to increase the execution speed on multi-core processors. In this case, you can use the parallel aggregation pattern illustrated below if the following conditions are satisfied:

1. The task can be split into multiple, independent parts, each producing a partial result
2. The result of one part is not dependent on the result of another part
3. The set of partial results from each worker thread can be combined (aggregated) when all the threads have finished into a final result
4. The communication between worker threads is minimal-to-none

The last requirement is a reformulation of the first one: if the threads keep stalling to wait for each other, they are not fully independent, and the speed gain may not be worth it for the added complexity.

Generally, any process that you split into parts must be somewhat re-engineered to work in parallel. The way to do this is highly algorithm-dependent. Here I have gone for a classic problem of adding a large sequence of numbers, but you can easily re-purpose this to perform any arithmetical operation on any disparate sets of data where partial results can be combined.

Designing the algorithm

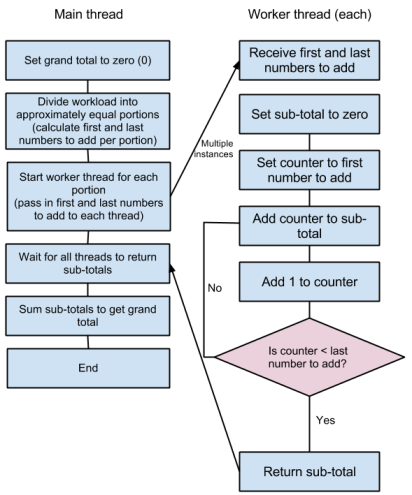
Figure 2. Adding all the numbers in a contiguous sequence, split across several threads, using aggregated sub-totals

Figure 1 shows the classic approach to adding a sequence of numbers in a single-threaded application. It is essentially nothing more than a simple for loop with a variable storing the running total so far. When the for loop completes, the running total becomes the final total, which is the answer to the calculation.

Figure 2 shows how we might split this up across multiple threads. We apportion a block of numbers to add together to each thread. The threads run in parallel and return their own sub-totals. The main thread then adds these sub-totals to get the grand total. Notice that this actually requires more additions than the single-threaded approach (specifically, the sub-totals must be added at the end, so if it is split across 4 threads, there will be 3 more additions), but these additions are a tiny fraction of the total work and do not translate into any meaningful performance hit.

Setting up your build environment correctly

Figure 3. Adding a new target architecture to your solution in Visual Studio

When people with multi-core processors start dabbling, they often wonder why their new code seems to run so slowly. Be warned! Make sure you do two essential things before speed-testing your algorithms:

1. Change the build configuration to Release if using Visual Studio – this turns on various compiler optimizations and turns off various debugging bottlenecks and other choke points.
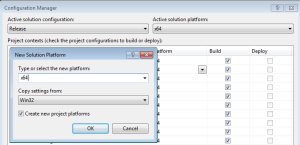
2. Target the correct processor architecture! If you are building for 32-bit platforms, the default Win32 target will be sufficient. If, however, you are building for 64-bit platforms, you should add a 64-bit target in Configuration Manager as shown in figure 3. From the Visual Studio main menu, simply choose Build -> Configuration Manager, then click the Active solution platform drop-down, choose New… and select x64 from the platform drop-down. You should see something similar to that in figure 3. Click OK and close the Configuration Manager, then you are good to go.

Single-threaded implementation and why it matters

Adding all of the numbers from 0 to 999,999,999 inclusive is very simple, and using either the uint64_t type in C++11 or boost::uint64_t, we can store the correct result. Something like this should do the trick:

#include <iostream>
#include <cstdint>  // for std::uint64_t

const int max_sum_item = 1000000000;

int main()
{
  std::uint64_t result = 0;

  for (int i = 0; i < max_sum_item; i++)
    result += i;

  std::cout << result;
}

Boost users: replace #include <cstdint> with #include <boost/cstdint.hpp> and all references to std::uint64_t with boost::uint64_t to make the example code work

First of all, it’s important to have some known correct answers to your algorithm or other test cases if at all possible, so that you can compare the results of any aggregated version to a single-threaded known working version. There is no question that the code above will work correctly – the only minor concern being that result‘s value type is wide enough (in bits) to store the total (the correct answer, by the way, is 499,999,999,500,000,000).

Secondly, we can find out how long the single-threaded version takes to execute, which is also very important as we will want to see if our multi-threaded version brings useful performance benefits or not – a poor implementation may be even slower than the single-threaded version!

Platform-independent measurement of time with C++11

As we may be working with milliseconds or even microseconds in extreme cases, we are going to need an accurate clock. C++11 introduces the chrono library which provides the high_resolution_clock static object which can be used to mark time and calculate the difference between two time points.

The idea goes like this:

#include <chrono>
...

auto start = std::chrono::high_resolution_clock::now();
// do something time-consuming
auto end = std::chrono::high_resolution_clock::now();

double timeTakenInSeconds = (end - start).count() * ((double) std::chrono::high_resolution_clock::period::num / std::chrono_high_resolution_clock::period::den);

The call to now() returns a time_point object. When the two time points are subtracted – returning a duration object – the method count() converts it to a double. Since we used the high resolution clock, the duration will be an amount of time elapsed in ticks; the number of ticks per second is architecture-dependent, but the conversion from ticks to seconds can be done by multiplying the tick count by the fraction period::num / period::den.  Hence, the calculation above takes the time a long task started and ended, and works out from those figures how long it took.

Applying this code to the single-threaded example above, the summation takes on average 0.22 seconds to complete on my Core i7-2600K with 6GB of DDR-1600 RAM when built in Release mode and targeting x64 as the architecture.

Platform-independent measurement of time with Boost

To measure time accurately with Boost, you can use Boost.DateTime. It looks something like this:

#include <boost/date_time/posix_time/posix_time.hpp>
...

boost::posix_time::ptime start = boost::posix_time::microsec_clock::local_time();
// do something time-consuming
boost::posix_time::ptime end = boost::posix_time::microsec_clock::local_time();

boost::posix_time::time_duration timeTaken = end - start;
std::cout << timeTaken << std::endl;

Note that time_duration has a number of methods to allow you to fetch the number of seconds, milliseconds, microseconds used etc. as a remainder fraction or total, but sending it to the console will automatically convert it into a nice human-readable string.

NOTE: Boost also includes the Boost.Chrono library which was implemented in the C++11 standard library and has identical syntax to the C++11 example above; simply replace std with boost.

Single worker thread

There are two main tasks here:

1. Move the calculation itself off into a standalone function
2. Make main() create the worker thread (which will execute the calculation function) and wait for it to return

Thread functions cannot return results directly, so instead you must pass a pointer to where you want the result to be stored. Our initial stab at the function looks like this:

#include <iostream>
#include <cstdint>
#include <thread>    // for std::thread

const int max_sum_item = 1000000000;

void do_sum(std::uint64_t *total)
{
  *total = 0;

  for (int i = 0; i < max_sum_item; i++)
    *total += i;
}

main() will now look like this:

int main()
{
  uint64_t result;
  std::thread worker(do_sum, &result);
  worker.join();

  std::cout << result << std::endl;
}

Boost users: Replace #include <thread> with #include <boost/thread.hpp> and all references to std::thread with boost::thread to make the code work identically to the C++11 example above.

Creating a thread is very simple: you simply create an instance of std::thread, passing in the name of the function to call and an arbitrary length list of arguments to pass to it. Execution begins in the worker thread as soon as it has been created, from the start of the named function.

Waiting for a thread to terminate is similarly trivial in this case: you just call join() on the std::thread object.

Seems simple enough, but wait, what’s this? Trying the code above on the same Core i7-2600K with 6GB of DDR-1600 RAM as the single-threaded example, with std::chrono applied, the average execution time soars to a whopping 1.06 seconds – a near five-fold decrease in performance. Why? The culprit is in do_sum(). In every round of the for loop, we de-reference the pointer to total, and it turns out this takes much longer than the calculation itself. The solution is to store the total locally in the function and only write it to the pointer at the end:

void do_sum(std::uint64_t *total)
{
  std::uint64_t localTotal = 0;

  for (int i = 0; i < max_sum_item; i++)
    localTotal += i;

  *total = localTotal;
}

This brings the average execution time back down to around 0.26 seconds on my machine – the extra time is accounted for by creating and deleting the worker thread, which are expensive operations. Note that this is a really classic and important example of how easily things can go awry even when a simple function seems perfectly innocent. Always work through your code step by step in this way when moving data algorithms from a single-threaded to multi-threaded model, and profile its speed at each step to make sure you are still getting the performance you expect.

Multiple worker threads (parallel aggregation)

Now we come to the meat of the problem: the implementation of the process shown in figure 2 above.

At the start of the program, we define the number of threads to use and a vector of uint64_t pointers to hold the partial result (the sub-total) from each worker thread, and in main() we allocate memory for the sub-totals before the worker threads are started:

#include <vector>

std::vector<uint64_t *> part_sums;
const int threads_to_use = 2;
...
int main()
{
  part_sums.clear();

  for (int i = 0; i < threads_to_use; i++)
    part_sums.push_back(new uint64_t(0));

Immediately after that, we create a vector of std::thread pointers to store the thread handles (objects):

  std::vector<std::thread *> t;

We now split up the work into equal chunks for each thread. Since we have 1 billion additions to do, we can easily calculate how much work to give to each thread (how many additions each thread will perform) by dividing the total number of additions by the number of threads to use. In this case using two threads, we’ll get 500 million calculations per thread:

  int sums_per_thread = max_sum_item / threads_to_use;

(see the next section below for an important problem with this and the solution)

So that each worker thread sums the correct set of numbers, we must provide two additional parameters to do_sum() than in the single-threaded version: the number to start at and the number of additions to do (or you could use the number to end at). For clarity, we rename the function to do_partial_sum and it looks like this:

void do_partial_sum(uint64_t *final, int start_val, int sums_to_do)
{
	uint64_t sub_result = 0;

	for (int i = start_val; i < start_val + sums_to_do; i++)
		sub_result += i;

	*final = sub_result;
}

As in the single worker thread example above, we are careful to use a local variable to store the sub-total and only write it to the de-referenced pointer at the end, for performance reasons.

We can now call do_partial_sum() to perform partial calculations (if we were using a single thread) as follows:

// do the calculation in 4 parts in a single thread
do_partial_sum(part_sums[0], 0, 250000000);
do_partial_sum(part_sums[1], 250000000, 250000000);
do_partial_sum(part_sums[2], 500000000, 250000000);
do_partial_sum(part_sums[3], 750000000, 250000000);

Of course, we need these functions to run in their own threads, so we roll it up into a for loop like this:

for (int start_val = 0, i = 0; start_val < max_sum_item; start_val += sums_per_thread, i++)
{
  t.push_back(new std::thread(do_partial_sum, part_sums[i], start_val, sums_per_thread));
}

Boost users: Replace std::thread with boost::thread to make the code work identically to the C++11 example above.

Now we wait for all of the threads to finish:

for (int i = 0; i < threads_to_use; i++)
   t[i]->join();

The join() method blocks and relinquishes control to the operating system while the main application thread is sleeping, so the machine doesn’t stall. When a worker thread finishes, join() returns. Therefore, this loop will only exit once all of the threads have terminated.

We now add together the sub-totals to get the grand total. The code below requires #include <algorithm> and uses the C++11 lambda expression syntax to iterate over each of the sub-totals and add them together:

uint64_t result = 0;

std::for_each(part_sums.begin(), part_sums.end(),
    [&result] (uint64_t *subtotal) { result += *subtotal; });

There are various other ways of doing this if you prefer.

We now have the correct result in result. Finally, clean up the allocated memory:

for (int i = 0; i < threads_to_use; i++)
{
  delete t[i];
  delete part_sums[i];
}

You can instead use ptr_vectors if you wish to avoid doing the memory management yourself.

The benefit of using just 2 worker threads in the example above is immediately apparent: on the same benchmark machine as before, the average computation time is now reduced to 0.17 seconds vs 0.26 seconds in the version with one worker thread.

Ensuring the final work unit is the right size

There is a crucial problem with our crude work-apportioning division formula above. It works fine when the number of threads is exactly divisible into the problem size (number of additions in this case); 1 billion is neatly divisible by 2, 4 or 8 threads; but what if you want 7 threads, or 54 threads? What if you want to sum a different series than 0-1 billion?

Consider the 7-threaded case: 1 billion divided into 7 chunks is 142,857,142.8 additions per thread. Obviously we can’t have .8 of an addition, and the int division will round this down to 142,857,142. This number of additions will be apportioned to each thread, leading to only numbers up to 999,999,994 being added, and giving the wrong result! One solution is to lump the extra few missing divisions onto the work of the last thread. We can do so with a bit of mathematical trickery inside the loop which starts the threads:

int sums_per_thread = max_sum_item / threads_to_use;

for (int start_val = 0, i = 0; start_val < max_sum_item; start_val += sums_per_thread, i++)
{
	// Lump extra bits onto last thread if work items is not equally divisible by number of threads
	int sums_to_do = sums_per_thread;

	if (start_val + sums_per_thread < max_sum_item && start_val + sums_per_thread * 2 > max_sum_item)
		sums_to_do = max_sum_item - start_val;

	t.push_back(new std::thread(do_partial_sum, part_sums[i], start_val, sums_to_do));

	if (sums_to_do != sums_per_thread)
		break;
}

The if statement checks whether the total amount of work (additions) remaining to be apportioned is more than that which would normally be apportioned to one thread, but less than what would be apportioned to two threads, meaning that this will be the final thread to create but there are also some left-over calculations to be done. If so, the number of additions to perform on this final thread is changed from the standard amount to whatever is remaining, by subtracting the current addition start value from the total number of additions in the entire calculation. In our 7-thread example, start_val at this point will be 857,142,852. The amount of work to assign per thread is 142,857,142 additions. If we add these together (start_val and sums_per_thread), we get 999,999,994, meaning that we are about to create the final thread, but the standard amount of work isn’t enough to finish the summation. So, we re-calculate the amount of work to apportion to the final thread as 1,000,000,000 – 857,142,852 which is 142,857,148 – providing exactly the extra 6 additions we need to finish the summation.

Notice the thread creation line now uses sums_to_do and not sums_per_thread when passing in the number of additions to do to the thread function.

The test at the end of the loop with the break statement is necessary to cause the loop to exit when the first non-standard work unit size is apportioned; remember that if we allowed the loop to repeat once more, start_val would be 999,999,994 and another thread would be incorrectly created, so we avoid that situation by breaking out of the loop once the remaining work has been lumped onto the last thread.

Testing result accuracy

Since parallel aggregation is full of quirks like the one above, it’s always a smart idea to check your results with some test cases. An easy way to do this is to use C++’s assert macros to help you (use #include <cassert>):

assert(result == uint64_t(499999999500000000));

The assert macro triggers an exception (or the debugger) if its argument evaluates to false. In our example, if you now change threads_to_use to 7, you should find that the macro is not triggered because the result is correct, but if you try it with the original version of the main for loop, the result will be wrong and an assertion failure will occur (an application crash with a dialog box showing the assert expression which failed).

Tracing thread execution

It’s often useful to see when threads start and end, what data is being passed in, what the partial results are and how long a thread took to complete its work. You can simply output text to cout or a file stream, but as discussed in the first part of this series, stream operations in C++ are not atomic so you must wrap their use in a synchronization object.

C++11 users can include the mutex library and create a globally scoped mutex at the start of the application like this:

#include <mutex>

std::mutex coutmutex;

Boost users don’t need to include a mutex library specifically as boost/thread.hpp includes it for you, so all you need is:

boost::mutex coutmutex;

You can then re-write do_partial_sum() to output various information:

void do_partial_sum(uint64_t *final, int start_val, int sums_to_do)
{
	coutmutex.lock();
	std::cout << "Start: TID " << std::this_thread::get_id() << " starting at " << start_val << ", workload of " << sums_to_do << " items" << std::endl;
	coutmutex.unlock();

	auto start = std::chrono::high_resolution_clock::now();

	uint64_t sub_result = 0;

    for (int i = start_val; i < start_val + sums_to_do; i++)
        sub_result += i;

    *final = sub_result;

    auto end = std::chrono::high_resolution_clock::now();

	coutmutex.lock();
	std::cout << "End  : TID " << std::this_thread::get_id() << " with result " << sub_result << ", time taken "
		<< (end - start).count() * ((double) std::chrono::high_resolution_clock::period::num / std::chrono::high_resolution_clock::period::den) << std::endl;
	coutmutex.unlock();
}

Boost users: Replace std::chrono with boost::chrono (or use boost::posix_time as described earlier) and std::this_thread::get_id() with boost::this_thread::get_id() to make the code work identically to the C++11 example above.

As you can see, you can get the current thread ID with std::this_thread::get_id(). A thread ID is a unique system-wide identifier for each thread running (or suspended) on the system.

Notice that all uses of std::cout must be wrapped in mutex locks as provided by the lock() method of std::mutex (or boost::mutex).

It’s important to understand that this kind of tracing has significant performance implications and should not be included in non-debug builds for the following reasons:

1. Writing to streams is computationally expensive compared to the relatively trivial additions we are doing
2. Locking the mutex in one thread will cause all of the other starting threads to stall until it is released, as they wait to write to the stream; similarly the stream write at the end of the function will stall all the other worker threads from exiting or starting.

Here are example outputs on the benchmark machine with 1, 2 and 7 threads (by changing the value of threads_to_use):

1 thread

Start: TID 8864 starting at 0, workload of 1000000000 items
End : TID 8864 with result 499999999500000000, time taken 0.288017
Result is correct
Time taken: 0.294017

2 threads

Start: TID 15296 starting at 0, workload of 500000000 items
Start: TID 10556 starting at 500000000, workload of 500000000 items
End : TID 10556 with result 374999999750000000, time taken 0.146008
End : TID 15296 with result 124999999750000000, time taken 0.164009
Result is correct
Time taken: 0.17101

7 threads

Start: TID 12688 starting at 0, workload of 142857142 items
Start: TID 13864 starting at 142857142, workload of 142857142 items
Start: TID 9256 starting at 285714284, workload of 142857142 items
Start: TID 3208 starting at 428571426, workload of 142857142 items
Start: TID 14636 starting at 571428568, workload of 142857142 items
Start: TID 11260 starting at 714285710, workload of 142857142 items
Start: TID 12132 starting at 857142852, workload of 142857148 items
End : TID 13864 with result 30612244459183675, time taken 0.0440025
End : TID 12688 with result 10204081438775511, time taken 0.0740042
End : TID 11260 with result 112244896540816331, time taken 0.0580033
End : TID 3208 with result 71428570500000003, time taken 0.0740042
End : TID 9256 with result 51020407479591839, time taken 0.0790046
End : TID 14636 with result 91836733520408167, time taken 0.0750043
End : TID 12132 with result 132653065561224474, time taken 0.0590033
Result is correct
Time taken: 0.116007

Notice that the 1-thread version calculates the entire correct result on its own; the 7-thread version assigns 6 extra additions to the last-created thread (ID 12132 in this example), and the 2 and 7-thread versions have thread execution which overlaps in time; while some threads have taken 0.07 seconds and others 0.05 or 0.04, the total time was only 0.116 seconds for 7 threads.

Full source code so far

For clarity, here is the full source code so far. I have added a #define to enable or disable console output (tracing). Comment this out to disable tracing.

C++11 version

#include <iostream>		// for std::cout
#include <cstdint>		// for uint64_t
#include <chrono>		// for std::chrono::high_resolution_clock
#include <thread>		// for std::thread
#include <vector>		// for std::vector
#include <algorithm>	// for std::for_each
#include <cassert>		// for assert

#define TRACE

#ifdef TRACE
#include <mutex>		// for std::mutex

std::mutex coutmutex;
#endif

std::vector<uint64_t *> part_sums;
const int max_sum_item = 1000000000;
const int threads_to_use = 7;

void do_partial_sum(uint64_t *final, int start_val, int sums_to_do)
{
#ifdef TRACE
	coutmutex.lock();
	std::cout << "Start: TID " << std::this_thread::get_id() << " starting at " << start_val << ", workload of " << sums_to_do << " items" << std::endl;
	coutmutex.unlock();

	auto start = std::chrono::high_resolution_clock::now();
#endif

	uint64_t sub_result = 0;

    for (int i = start_val; i < start_val + sums_to_do; i++)
        sub_result += i;

    *final = sub_result;

#ifdef TRACE
    auto end = std::chrono::high_resolution_clock::now();

	coutmutex.lock();
	std::cout << "End  : TID " << std::this_thread::get_id() << " with result " << sub_result << ", time taken "
		<< (end - start).count() * ((double) std::chrono::high_resolution_clock::period::num / std::chrono::high_resolution_clock::period::den) << std::endl;
	coutmutex.unlock();
#endif
}

int main()
{
  part_sums.clear();

  for (int i = 0; i < threads_to_use; i++)
    part_sums.push_back(new uint64_t(0));

  std::vector<std::thread *> t;

  int sums_per_thread = max_sum_item / threads_to_use;

  auto start = std::chrono::high_resolution_clock::now();

  for (int start_val = 0, i = 0; start_val < max_sum_item; start_val += sums_per_thread, i++)
  {
    // Lump extra bits onto last thread if work items is not equally divisible by number of threads
    int sums_to_do = sums_per_thread;

    if (start_val + sums_per_thread < max_sum_item && start_val + sums_per_thread * 2 > max_sum_item)
        sums_to_do = max_sum_item - start_val;

    t.push_back(new std::thread(do_partial_sum, part_sums[i], start_val, sums_to_do));

    if (sums_to_do != sums_per_thread)
        break;
  }

  for (int i = 0; i < threads_to_use; i++)
    t[i]->join();

  uint64_t result = 0;

  std::for_each(part_sums.begin(), part_sums.end(), [&result] (uint64_t *subtotal) { result += *subtotal; });

  auto end = std::chrono::high_resolution_clock::now();

  for (int i = 0; i < threads_to_use; i++)
  {
    delete t[i];
    delete part_sums[i];
  }

  assert(result == uint64_t(499999999500000000));

  std::cout << "Result is correct" << std::endl;

  std::cout << "Time taken: " << (end - start).count() * ((double) std::chrono::high_resolution_clock::period::num / std::chrono::high_resolution_clock::period::den) << std::endl;
}

C++03-compliant version using Boost

#include <iostream>					// for std::cout
#include <boost/cstdint.hpp>		// for boost::boost::uint64_t
#include <boost/chrono.hpp>			// for boost::chrono::high_resolution_clock
#include <boost/thread.hpp>			// for boost::thread and boost::mutex
#include <vector>					// for std::vector
#include <cassert>					// for assert

#define TRACE

#ifdef TRACE

boost::mutex coutmutex;
#endif

std::vector<boost::uint64_t *> part_sums;
const int max_sum_item = 1000000000;
const int threads_to_use = 7;

void do_partial_sum(boost::uint64_t *final, int start_val, int sums_to_do)
{
#ifdef TRACE
	coutmutex.lock();
	std::cout << "Start: TID " << boost::this_thread::get_id() << " starting at " << start_val << ", workload of " << sums_to_do << " items" << std::endl;
	coutmutex.unlock();

	boost::chrono::high_resolution_clock::time_point start = boost::chrono::high_resolution_clock::now();
#endif

	boost::uint64_t sub_result = 0;

    for (int i = start_val; i < start_val + sums_to_do; i++)
        sub_result += i;

    *final = sub_result;

#ifdef TRACE
    boost::chrono::high_resolution_clock::time_point end = boost::chrono::high_resolution_clock::now();

	coutmutex.lock();
	std::cout << "End  : TID " << boost::this_thread::get_id() << " with result " << sub_result << ", time taken "
		<< (end - start).count() * ((double) boost::chrono::high_resolution_clock::period::num / boost::chrono::high_resolution_clock::period::den) << std::endl;
	coutmutex.unlock();
#endif
}

int main()
{
  part_sums.clear();

  for (int i = 0; i < threads_to_use; i++)
    part_sums.push_back(new boost::uint64_t(0));

  std::vector<boost::thread *> t;

  int sums_per_thread = max_sum_item / threads_to_use;

  boost::chrono::high_resolution_clock::time_point start = boost::chrono::high_resolution_clock::now();

  for (int start_val = 0, i = 0; start_val < max_sum_item; start_val += sums_per_thread, i++)
  {
    // Lump extra bits onto last thread if work items is not equally divisible by number of threads
    int sums_to_do = sums_per_thread;

    if (start_val + sums_per_thread < max_sum_item && start_val + sums_per_thread * 2 > max_sum_item)
        sums_to_do = max_sum_item - start_val;

    t.push_back(new boost::thread(do_partial_sum, part_sums[i], start_val, sums_to_do));

    if (sums_to_do != sums_per_thread)
        break;
  }

  for (int i = 0; i < threads_to_use; i++)
    t[i]->join();

  boost::uint64_t result = 0;

  for (std::vector<boost::uint64_t *>::iterator it = part_sums.begin(); it != part_sums.end(); ++it)
	  result += **it;

  boost::chrono::high_resolution_clock::time_point end = boost::chrono::high_resolution_clock::now();

  for (int i = 0; i < threads_to_use; i++)
  {
    delete t[i];
    delete part_sums[i];
  }

  assert(result == boost::uint64_t(499999999500000000));

  std::cout << "Result is correct" << std::endl;

  std::cout << "Time taken: " << (end - start).count() * ((double) boost::chrono::high_resolution_clock::period::num / boost::chrono::high_resolution_clock::period::den) << std::endl;
}

The differences between the two are:

• Different #includes
• Replacement of std:: with boost:: where applicable
• Replacement of uint64_t with boost::uint64_t
• Replacement of auto with boost::chrono::high_resolution_clock::time_point
• Replacement of the C++11 lambda sub-total addition code with a standard vector iterator for loop:

for (std::vector<boost::uint64_t *>::iterator it = part_sums.begin(); it != part_sums.end(); ++it)
  result += **it;

Multi-core processors

Multi-core processors provide true hardware multi-threading or hardware concurrency, which means that rather than the threads being time-sliced by the OS, they are truly run in parallel, simultaneously. This gives any well-designed multi-threaded applications you create a massive performance boost, as without multi-threading your application will only use one available core by default.

As a rough rule of thumb, the OS does a 1-to-1 mapping of your application threads to cores; that is to say, if you use 4 threads and there are 4 cores available, one thread will run on each core. If all the cores are in use, the OS will generally schedule new threads on the current least busiest cores (the ones under the least CPU load). A normal Windows machine will typically have anything from dozens to hundreds of threads running simultaneously even when the machine is idling on the desktop (you can see this in the Performance tab of Task Manager – right now the Windows 7 64-bit machine I am typing on has 1456 running threads, with many applications running (92 processes)). So, your threads will still get time-sliced, but generally speaking, on an N-core processor, they will be woken up N times more often than on a single-core processor. Note that the OS may reserve 1 or more cores for its own use, so the optimum number of threads to use isn’t necessarily the total number of CPU cores available.

In the first part of this series I mentioned Amdahl’s Law, which demonstrates that splitting your task into more threads or cores has a gradually diminishing return; there comes a point where performance plateaus no matter how many extra threads you use, and using more becomes pointless. See the link at the top of this article for more details.

Finding the optimum number of threads to use on a multi-core CPU

To find out programmatically how many processor cores the CPU your application is running on has, you can use std::thread::hardware_concurrency() (or boost::thread::hardware_concurrency()). Note this is the number of logical cores as seen by the OS; 4-core processors such as the Core i7 benchmark machine which also have hyper-threading enabled will self-report as 8-core processors (this isn’t really a problem, just something worth knowing).

By simply removing the const definition of threads_to_use and wrapping the entire contents of main() in our example above with a for loop like this:

for (int threads_to_use = 1; threads_to_use <= static_cast<int>(std::thread::hardware_concurrency()); threads_to_use++)
{
  // original code

  std::cout << "Time taken with " << threads_to_use << " core" << (threads_to_use != 1? "s":"") << ": " << (end - start).count() * ((double) std::chrono::high_resolution_clock::period::num / std::chrono::high_resolution_clock::period::den) << std::endl;
}

(use boost::thread::hardware_concurrency() instead if you are using Boost)

we can repeat the calculation using any number of worker threads from 1 to the number of cores available and see which runs fastest. On the benchmark machine, the results are interesting:

Time taken with 1 core: 0.295017
Time taken with 2 cores: 0.149008
Time taken with 3 cores: 0.131008
Time taken with 4 cores: 0.108006
Time taken with 5 cores: 0.108006
Time taken with 6 cores: 0.0920053
Time taken with 7 cores: 0.0820047
Time taken with 8 cores: 0.105006

As you can see performance increases somewhat logarithmically until we get to 7 cores, but with 8 cores in use performance drops off. This is because the OS reserves 1 core for its own use. Results are similar with 2 and 4-core CPUs, so we can conclude that for maximum performance the best number of cores to use is the number available minus one, but if you want to trade off a slight amount of performance, the best number of cores to use is about half that of the number available.

Operating System build, application build and hyper-threading detection for Windows

Fetching hyper-threading state

You can find out if the processor supports hyper-threading as follows (see my article on __cpuid for more details):

int cpuinfo[4];
__cpuid(cpuinfo, 1);

bool hasHT = (cpuinfo[3] & (1 << 28)) > 0;

Detecting the application and OS build targets

To find out if the application is a 32-bit or 64-bit build, and whether the system is using a 32-bit or 64-bit version of Windows, you can use the following code (see my article on 32 and 64-bit builds for more details):

#include <Windows.h>
...
#if defined(_WIN64)
	int app64 = true;
	int os64 = true;
#else
	int app64 = false;

	BOOL f64 = FALSE;
	int os64 = IsWow64Process(GetCurrentProcess(), &f64) && f64;
#endif

Results

Figure 4. Performance of our example application on 64-bit Windows in various build configurations

In figure 4 you can see the difference between running a 32-bit build on a 64-bit Windows, vs a native 64-bit build, with both Debug and Release build configurations in Visual Studio. All of the results use the Core i7-2600K benchmark machine. The chart was built by running the example in each configuration and plotting the results on a chart using Excel.

As you can see, there is a point of diminishing returns by adding more cores, and apart from the 32-bit debug build the performance tops off at 7 cores in all cases.

Performance between Release builds in 32-bit and 64-bit are roughly comparable when several cores are in use, but performance of the 1 and 2-core cases suffers dramatically when run on the 64-bit OS.

Try it yourself

Download the 32-bit and 64-bit versions of the example application.

What next?

In the final part of this series, we shall look at how to accomplish the same task using PPL, the Parallel Patterns Library for C++11, and the pros and cons of using it.

Good luck!